10082. Кратчайший
четный путь
Задан
неориентированный граф. Найдите кратчайший путь между двумя вершинами четной
длины.
Вход. Первая строка содержит четыре
целых числа: количество вершин n,
количество ребер m (n, m
≤ 105) и номера вершин s
и d (1 ≤ s, d ≤ n). Каждая из следующих m строк содержит два целых числа a и b
задающих неориентированное ребро (a, b).
Выход. Выведите кратчайший путь между
вершинами s и d. Длина пути (количество ребер в пути) должна быть четной. Если
пути четной длины между s и d не существует, то выведите -1.
|
Пример
входа 1 |
Пример
выхода 1 |
|
8 8 1 6 1 2 2 3 3 4 4 5 5 6 4 7 7 8 8 6 |
6 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
6 5 1 6 1 2 2 3 3 4 4 5 5 6 |
-1 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
Расщепим каждую
вершину v графа на две: v1 и v2. Для каждого
неориентированного ребра (u, v) создадим два неориентированных ребра (u1, v2)
и (u2, v1).

Например, можно
вершине v поставить в соответствие 2 * v – 1 и 2 * v.
Кратчайший путь
между вершинами 2 * s – 1 и 2 * d – 1 будет искомым и иметь четную длину.
Рассмотрим
следующий граф и соответствующий ему расщепленный.
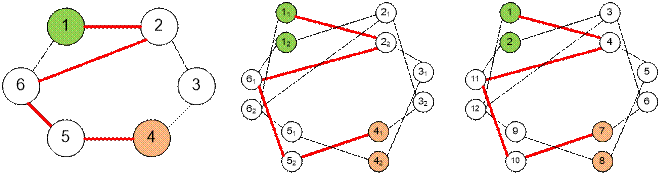
Пусть
поиск в ширину запущен из вершины v = 11. Тогда
·
если мы достигнем вершины x1, то длина пути бдет четной;
·
если мы достигнем вершины x2, то длина пути бдет нечетной;
Поиск
кратчайшего пути четной длины от 1 до 4 в исходном графе эквивалентен поиску кратчайшего пути от 11 до 41 (или от 1 до 7) в расщепленном
графе.
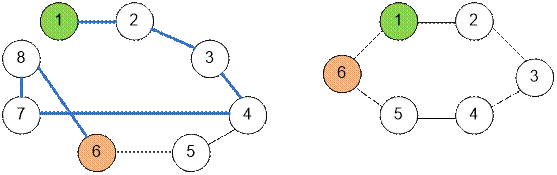
Пример
Граф,
приведенный в первом примере, показан слева. Четный кратчайший путь выделен. Во
втором примере (рисунок справа) между вершинами 1 и 6 не существует пути четной
длины.
Реализация алгоритма
Объявим список смежности g графа и массив
кратчайших расстояний dist.
vector<vector<int>
> g;
vector<int>
dist;
Функция bfs реализует поиск в ширину из вершины start.
void bfs(int start)
{
queue<int>
q;
q.push(start);
while
(!q.empty())
{
int v =
q.front(); q.pop();
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(dist[to] == -1)
{
q.push(to);
dist[to] =
dist[v] + 1;
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d %d",
&n, &m, &s, &d);
g.resize(2*n + 1);
for (i = 0; i < m; i++)
{
scanf("%d
%d", &u, &v);
Читаем ребро (u, v). Расщепляем каждую из вершин u и v на две.
Проводим ребра (2*u, 2*v – 1) и (2* v, 2*u – 1).
g[2*u].push_back(2*v-1);
g[2*v-1].push_back(2*u);
g[2*v].push_back(2*u-1);
g[2*u-1].push_back(2*v);
}
После расщепления количество вершин
увеличивается вдвое.
n = 2 * n;
Инициализируем массив кратчайших
расстояний.
dist = vector<int>(n
+ 1, -1);
dist[2*s-1] = 0;
Запускаем поиск в ширину из стартовой
вершины.
bfs(2*s-1);
Выводим ответ.
printf("%d\n",
dist[2*d-1]);
Java реализация
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int dist[];
static void bfs(int start)
{
Arrays.fill(dist,-1);
dist[start] =
0;
Queue<Integer> q = new
LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for(int i = 0;
i < g[v].size();
i++)
{
int to = g[v].get(i);
if (dist[to] ==
-1)
{
q.add(to);
dist[to] = dist[v] +
1;
}
}
}
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int s = con.nextInt();
int d = con.nextInt();
g = new
ArrayList[2*n+1];
for(int i = 0;
i <= 2*n; i++)
g[i] = new
ArrayList<Integer>();
for (int i = 0;
i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
g[2*u].add(2*v-1);
g[2*v-1].add(2*u);
g[2*v].add(2*u-1);
g[2*u-1].add(2*v);
}
n = 2
* n;
dist = new int[n+1];
bfs(2*s-1);
System.out.println(dist[2*d-1]);
con.close();
}
}